14 Vector Clocks
Lamport clock enforces a global total order, even if a and b are concurrent, there will still be timestamp where T(a) > T(b) or T(b) > T(a).
Vector clock acknowledges this downside, thus instead of global total order, enforces a partial casual order
v(a) = [x1, x2, x3, … xn]
- n, the # of processes in our system
- xj, the # of events that occured before a on process j
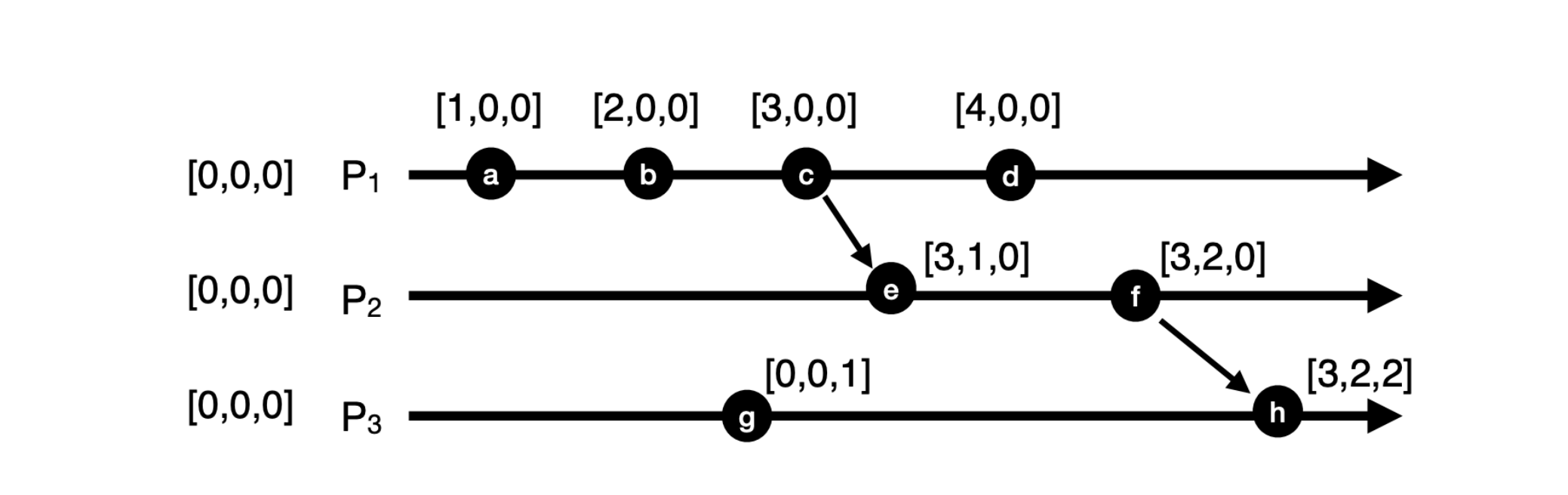
Vector Clock Process
Initially, v(a) = [0,0,0 … 0]
Three processes: P₁, P₂, P₃.
P₁: internal event →
[1,0,0]P₂: internal event →
[0,1,0](Both now independent — concurrent)P₁ → P₂: sends a message with
[1,0,0]
P₂ receives it:
Merge: max([0,1,0], [1,0,0]) =[1,1,0]
Increment own entry:[1,2,0]
So P₂’s vector now says: “I’ve seen 1 event from P₁, and 2 from myself.”
Vector timestamps are also comparable as follows:
Event p happened before Event q
if and only if:
vp[i]≤vq[i]for all i- there exist some k such that
vp[k]<vq[k]
Happened-before
If v(a) < v(b), then a → b.
If a → b, then v(a) < v(b)
Concurrency
If v(a) !> v(b) and v(a) !< v(b)
| Concept | What it tracks | Can tell concurrency? | Produces total order? | Matches real causality? |
|---|---|---|---|---|
| Happened-before | True causal reality | ✅ Yes | ❌ No | ✅ Perfectly |
| Lamport timestamps | Logical order (1D) | ❌ No | ✅ Yes | ❌ Partial |
| Vector timestamps | Per-process causal knowledge (nD) | ✅ Yes | ❌ No | ✅ Perfectly |
Causally-Ordered Multicast
We don't have to guarantee that one event happens before another, unless they actually have a casual order. Use vector timestamps to acheive this.