Cs440Wa4
1
1.1
function OracleMinimaxSearch(state, player):
if TERMINAL(state) then
return UTILITY(state)
if player == MAX then:
bestValue ← -∞
for each action a in ACTIONS(state) do:
newState ← RESULT(state, a)
value_a ← OracleMaxSearch(newState)
if value_a > bestValue then:
bestValue ← value_a
return bestValue
else if player == MIN then:
// Use the oracle to get the opponent’s optimal move.
opponent_action ← O(state)
newState ← RESULT(state, opponent_action)
return OracleMaxSearch(newState)
// helper
function BestMove(s0):
bestValue ← -∞
bestAction ← null
for each action a in ACTIONS(s0) do:
value_a ← OracleMaxSearch(RESULT(s0, a))
if value_a > bestValue then:
bestValue ← value_a
bestAction ← a
return bestAction
| Statement | Reason |
|---|---|
Base Case: If $s$ is terminal, OracleMaxSearch(state, player) = Utility(state, player)the minimax algoritm will also return Utility(state, plyaer). They are the same. | Directly from the pseudocode and definition of minimax, both behave the same when it comes to terminal nodes. |
assume for all states $t$ at depth $d$ or less , OracleMaxSearch(t, player) = Minimax(t, player). need must show it holds at depth $d+1$. | inductive step |
| Let $s$ be a state at depth $d+1$ where it is MAX’s turn. By definition, | For MAX moves |
| $\text{MinimaxValue}(state)$ = $\max_{a \in \text{Actions}(state)}$ $\min_{b \in \text{Actions}(\text{Result}(state,a))}$ $\text{MinimaxValue}(\text{Result}(\text{Result}(state,a), b), plyaer) ).$ | Standard minimax rule. and for conciseness, I will write Minimax(s) |
| By assumption of the oracle, for any state $s'$ (with MIN to move) we have $O(s') = b^$ where $b^$ satisfies: | The oracle returns MIN’s best move. |
| $b^* \in \arg\min_{b \in \text{Actions}(s')} \text{MinimaxValue}(\text{Result}(s', b), player).$ | since oracle is always correct |
| Hence, in the single‐player transformation, from state $s$, if MAX picks $a$, we move to $s' = \text{Result}(state,a)$, then the oracle’s move is $b^* = O(s')$. So the resulting state is $s'' = \text{Result}(s', b^*)$. | by the pseudocode. |
| $\min_{b \in \text{Actions}(s')} \text{MinimaxValue}(\text{Result}(s', b)) = \text{MinimaxValue}(\text{Result}(s', b^*)).$ | By definition of $b^*$. |
| Therefore | |
| $\text{MinimaxValue}(state) =$ $\max_{a \in \text{Actions}(state)} \text{MinimaxValue}(s''),$ $\text{ where } s'' = \text{Result}(\text{Result}(state,a), O(\text{Result}(state,a))).$ | Rewriting the minimax expression to factor in the oracle. |
By the inductive hypothesis, for each “child” $s''$ at depth $d$ (one level closer to terminal), OracleMaxSearch(s'') = MinimaxValue(s''). | apply induction assumption |
So, in computing OracleMaxSearch(state), we take the same maximum over exactly the same values $\text{MinimaxValue}(s'')$. | From the pseudocode’s recursion. |
Hence OracleMaxSearch(state, player) = MinimaxValue(state, player). | thus they are the same at depth $d+1$. |
| By mathematical induction on the depth, these two functions behave the same for all states $s$. | conclusion |
1.2
function OracleMaxSearchStochastic(state, player):
if TERMINAL(state) then
return UTILITY(state)
if NODE_TYPE(state) == CHANCE then:
expectedValue ← 0
for each outcome o in CHANCE_OUTCOMES(state) do:
//probability p(o) if each outcome
newState ← RESULT(state, o)
expectedValue ← expectedValue + p(o) *
OracleMaxSearchStochastic(newState)
return expectedValue
else if player == MAX then:
bestValue ← -∞
for each action a in ACTIONS(state) do:
newState ← RESULT(state, a)
value_a ← OracleMaxSearchStochastic(newState)
if value_a > bestValue then:
bestValue ← value_a
return bestValue
else if player == MIN then:
// use the oracle to get the opponent’s optimal action.
opponent_action ← O(state)
newState ← RESULT(state, opponent_action)
return OracleMaxSearchStochastic(newState)
| Statement | Reason |
|---|---|
| Simplify Minimax(state, player) to just Minimax(state) so that writing will be easier | |
| Base Case: For terminal state $s$, the algorithm simply returns $\text{UTILITY}(state)$ just like expectiminimax. | by definition |
| Inductive Hypothesis: Assume that for any state $s'$ at depth less than $n$, | Inductive hypothesis |
| $\text{OracleMaxSearchStochastic}(s')$ returns the correct value. | |
| Case 1: $s$ is a MAX node. | |
| The algorithm computes $\max_{a \in \text{ACTIONS}(state)} \text{OracleMaxSearchStochastic}(\text{RESULT}(state, a))$. | According the pseudocode, each successor is evaluated recursively and the maximum is chosen. |
| Case 2: $s$ is a MIN node. | |
| The algorithm calls the oracle $O(state)$ to get the optimal opponent action and returns $\text{OracleMaxSearchStochastic}(\text{RESULT}(state, O(state)))$. | Since the oracle is perfect, so it returns the opponent's best move. |
| Case 3: $s$ is a chance node. | |
| The algorithm computes the expected value: $\sum_{o \in \text{CHANCE_OUTCOMES}(state)} p(o)$ x $\text{OracleMaxSearchStochastic}(\text{RESULT}(state, o))$. | This is the definition of expected value. By the inductive hypothesis, the value for each outcome is correctly computed. |
| Conclusion: For every type of node (MAX, MIN, or CHANCE), the algorithm computes the correct value for state $s$. | Thus by induction, the algorithm correctly computes the optimal value for the initial state $s_0$. |
2
2.1
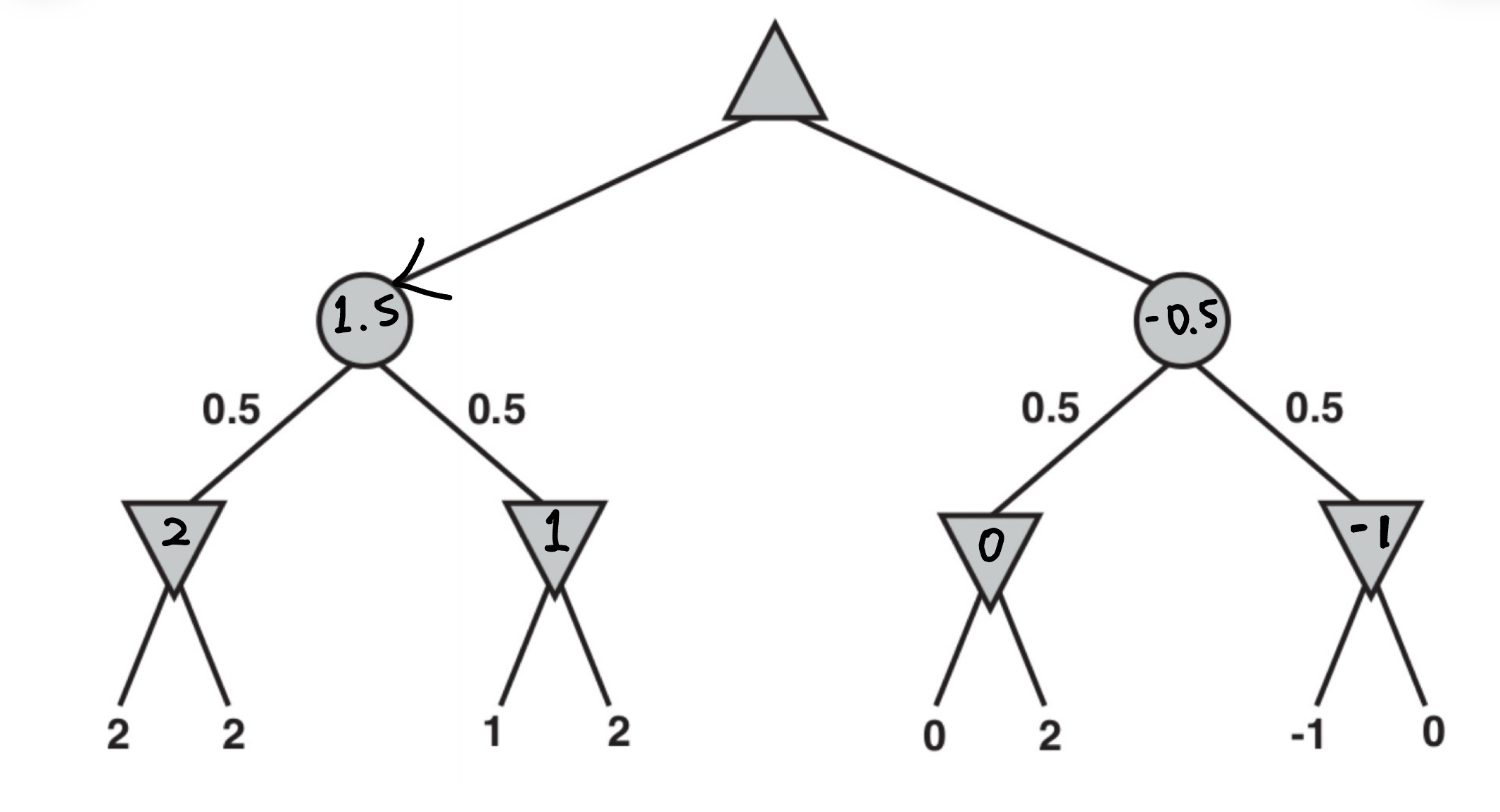
2.2
If you have already observed the first six leaf nodes, do we need to evaluate the seventh and eighth leaves in order to determine the value of the parent CHANCE node?
Yes. take for example say If the seventh node and the eighth nodes are extremely large, then we would go to the right chance node instead.
What if we’ve observed the first seven leaves, do we need to observe the eighth in order to determine the value of the parent CHANCE node? Note: this is not a proof.
Sometimes yes and sometimes no. if we already know that leaf 7 turned out to be very small, and the MIN of {7,8} cannot be larger than that, there's no need to know. However, If leaf 7 is large enough that the right MIN child could still beat (or tie) the left CHANCE node, we do need to look at leaf 8, because the MIN of a large number and an unknown number is unknown.
2.3
if the second two leaves are both the lowest, -2, and -2, we get 0 in the chance node. If they're both largest, 2, and 2, we get 2 in the chance node. so the range is [0,2]
2.4
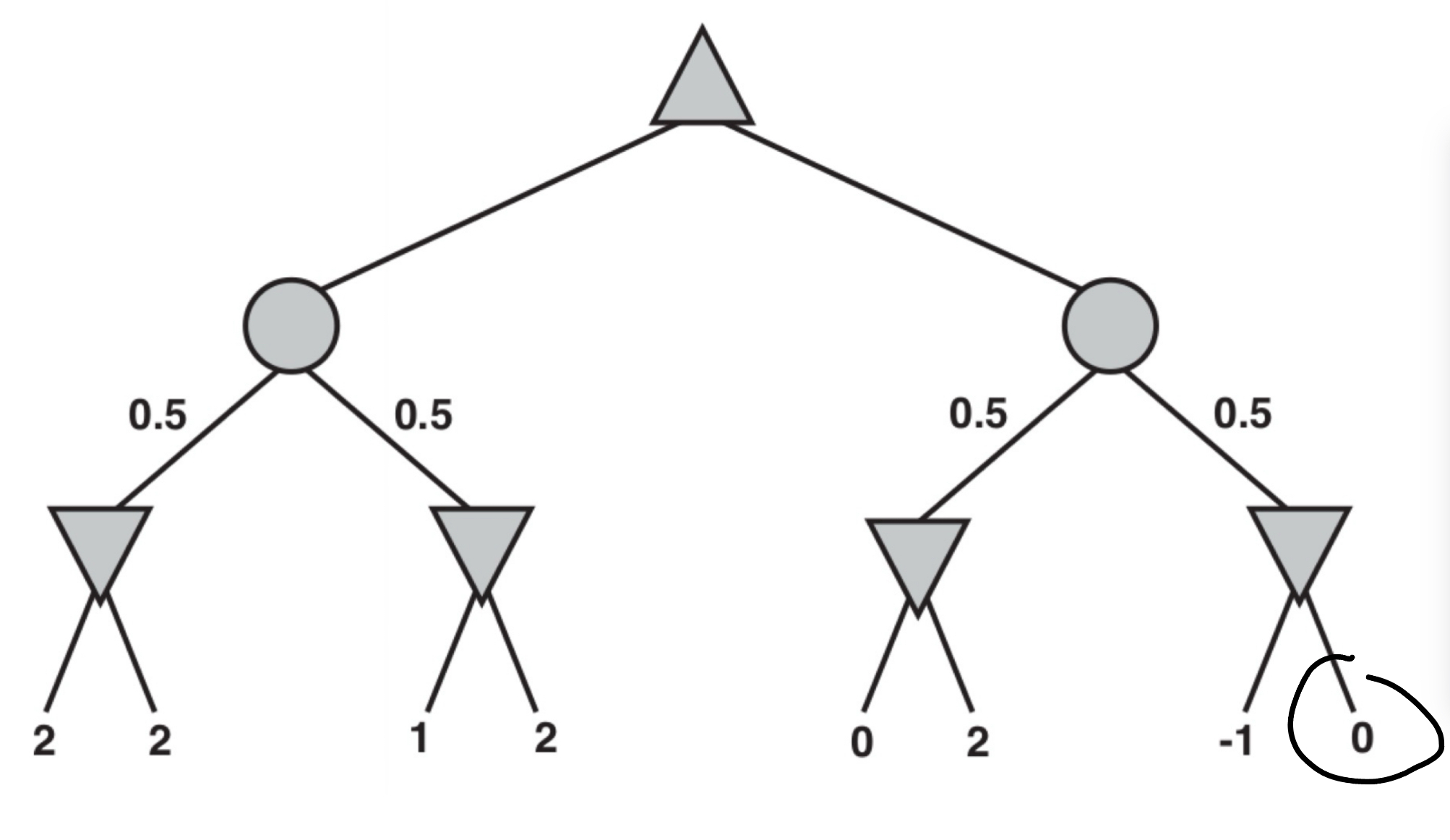
When we get to the right CHANCE node (the one on the right), we first evaluate its left MIN child (from leaves “0” and “2”) and find its value is 0.
Next we start evaluating its right MIN child. When we see its first leaf, –1, we know that the MIN operator will take the smaller of (–1, L8). But since L8 can be at best +2, the best (i.e. highest) that MIN could ever be is –1 (if L8 ≥ –1).
Thus, the value of the right CHANCE node will be at most -0.5.
which is strictly less than the left CHANCE node’s value (1.5). In other words, no matter what L8 turns out to be, this branch cannot beat the left branch at the root. Thus we can prune L8.
3
| Statement | Reason |
|---|---|
| if s is a terminal node, then by definition, $v = utility(s) = v'$ So all three properties hold | base case |
| Assume the claim holds for all children of s. We consider the two cases: when s is a MAX node and when it is a MIN node. | inductive step |
| let the children of s be s1, s2, ... , sn with true minimax values v1, v2... vn, so that v=max vi. | Case 1. s is a MAX node |
| the algorithm recursively computes = Alpha-Beta(si,α,β) by updating alpha with the greater $v'$ | For each child si |
| If the true value $v_i$ lies in the current bounds then $v_i' = v_i$. | By the inductive hypothesis |
| If $v_i \le \alpha$ then $v_i' \le \alpha$. | |
| If $v_i \ge \beta$ then $v_i' \ge \beta$. | |
| Since $v = \max_i v_i$ and none of the children’s values force a cutoff (i.e. none of them are so high as to make $v \ge \beta$), every child is fully evaluated and, by the inductive hypothesis, $v_i' = v_i$. | If $\alpha \le v \le \beta$: |
| $v' = \max_i v_i' = \max_i v_i = v.$ | Hence |
| In this case every child has $v_i \le \alpha$, so by the inductive hypothesis, $v_i' \le \alpha$. Thus the MAX over them will also be at most $\alpha$, so $v' \le \alpha$. | If $v \le \alpha$, by the induction hypothesis |
| In this case, while processing the children, as soon as one child returns a value $v_i' \ge \beta$ the algorithm will update $\alpha$ and then prune the remaining children. Thus, the algorithm returns some $v' \ge \beta$. | If $v \ge \beta$ |
| let the children of s be s1, s2, ... , sn with true minimax values v1, v2... vn, so that v=min vi. | Case 2. s is a MIN node |
| the algorithm recursively computes = Alpha-Beta(si,α,β) by updating beta with the smaller $v'$ | for each child |
| $v' = \min_i v_i' = \min_i v_i = v$ | If $\alpha \le v \le \beta$: |
| In this case, while processing the children, as soon as one child returns a value $v_i' \le \alpha$ the algorithm will update (\beta) and then prune the remaining children. Therefore, the algorithm returns some $v' \le \alpha$. | If $v \le \alpha$ |
| In this case every child has $v_i \ge \beta$ so by the inductive hypothesis $v_i' \ge \beta$ Thus, $v' = \min_i v_i' \ge \beta$ | If $v \ge \beta$ |
| for any state $s$ the following properties hold: - If $\alpha \le v \le \beta$ then $v' = v$. - If $v \le \alpha$ then $v' \le \alpha$. - If $v \ge \beta$ then $v' \ge \beta$. | Thus, by induction |